切入法锥齿轮磨削

　　在锥齿轮生产领域，近年来的研究重点主要集中在铣削加工上。针对直齿锥齿轮磨削，建立了磨削烧伤风险预测的经验模型-工艺参数。然而，由于没有进行建模，结果只适用于非常有限的部件和砂轮范围。锥齿轮磨削中切削力的测量和预测目前还没有相关的研究。

　　切入法磨削锥齿轮的切削力和主轴磨削功率。磨削过程中经常使用的模型是力模型。最初，这个模型是为表面磨削加工而开发的。对于磨齿，已经采用了这种计算方法。在以前的计算中，具体法向磨削力Fn'是根据公式1计算的。

　　在研究中，本文作者研究了Werner模型是否可以用于锥齿轮磨削过程工艺。为了将Werner磨削的受力模型转化为磨削锥齿轮的受力模型，分析了切入式磨削锥齿轮的接触条件。以某重型汽车被动齿轮为例，计算了切削速度和切屑截面随时间的变化情况。对于精磨削过程，几乎可以确定平均材料去除率随时间几乎恒定。在接触条件的基础上，将Werner的切削力模型应用于切入法加工的锥齿轮磨削工艺。

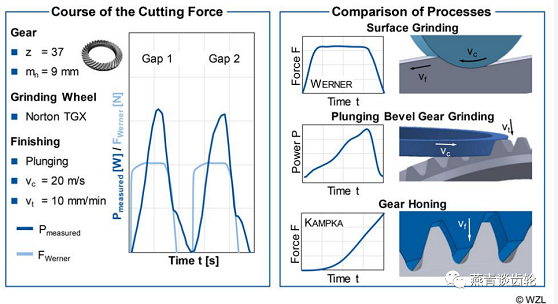
　　通过传递模型和确定接触条件，推导出切入法锥齿轮磨削的期望力曲线，如图6左侧所示。根据Werner的预期力曲线与测量的刀具主轴功率进行定性比较。对测量到的主轴功率信号的研究表明，尽管在理论上几何和运动接触条件近似恒定，但在此过程中功率显著增加，见图6。这种增加很可能是由切削力的增加引起的，因为切削力通常被认为与刀具主轴功率成正比。

　　这种切削力的增加不能直接由Werner模型预测，该模型主要考虑几何和运动学条件，接触区没有材料变化和弹性影响。切削力的增加,尽管理论上也可以确定珩齿存在几乎恒定的几何和运动学接触条件。磨削过程之间的主要区别，Werner模型可以应用整个过程持续时间和切入法锥齿轮加工以及珩齿的主要进给方向。在仿形磨削和直齿磨削中，主要的进给部件指向齿宽方向，而进给材料则在齿隙外进行。在直齿锥齿轮磨削和珩齿中，进给量在齿高进入材料的方向上是连续的，导致每道刀具进给量只有几微米。

　　由于连续的进给加工过程中，相同面积的齿面被反复加工，不断增加切入深度。如果工件-刀具-机床系统在磨削过程中发生弹性变形，则不会对整个被加工的工件进行加工。如果理论工件加工余量不足，则增加下一个要加工的材料会出现砂轮破碎，导致加工所需的切削力增加。

　　在坐标变换的帮助下，测量的力信号被转移到齿侧。这些分量被分为一个切向力Ft(平行于刀翼和刀具旋转的分量)和一个垂直于齿廓的法向力Fn。对于凸面磨削，切削力分量为切向力Ft、法向力Fn和同时测量的功率如图7所示。

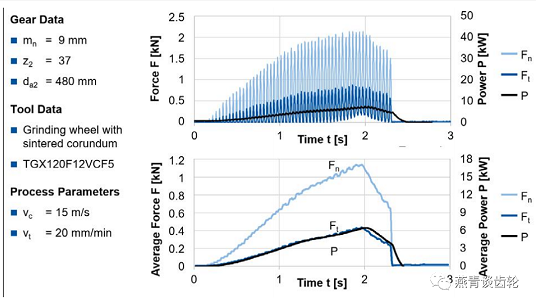
　　从图中可以看出，法向力Ft在切削力中所占比例最大。这符合平面磨削和轮廓齿轮磨削的先进水平。力分量的过程最初显示出增加，同时达到最大值。测量的主轴功率以可比较的方式增加。上升的开始和功率的最大值的达到与力相比有轻微的延迟。切削力分量和主轴功率的增加几乎相同，这证实了之前确定的切入法锥齿轮磨削主轴功率的增加，见图1。这证实了一个假设，即在切入法锥齿轮的过程中切削力会增加，尽管磨削中材料的去除率几乎保持不变。

　　各力曲线均表现出与偏心运动频率相对应的频率f= 1500/ min的振荡。对于单面磨削，可以看到在开始加工时，每转动一次偏心轴切削力分量在最大值到零之间变化。因此，假设在单面磨削过程中，偏心运动导致砂轮在每次旋转中完全失去接触。测量到的信号还表明，在t=1.7秒的加工时间后，切削力水平没有回到零。由于运动学特性保持不变，这是一个弹性变形的指标，这在早期的研究中已经假设。

　　由于工件-刀具-机床系统的灵活性，在接触区产生弹性变形，这意味着被磨削的工件没有被完全加工。这可能导致砂轮不再完全离开啮合，尽管仍旧存在重叠偏心运动。弹性变形的另一个标志是切削力在到达最终深度后并没有立即降为零。由于系统的弹性变形，并不是所有的理论切削材料立即被切削，在切入法锥齿轮磨削过程结束后，砂轮必须留在齿槽中。在此停留时间内，剩余的余量是在一个恒定的进给深度加工，与切削力近似线性下降。

　　最后，本文提出的力测量方法证实了锥齿轮磨削过程中存在显著的弹性变形。进一步验证了锥齿轮磨削过程中刀具主轴功率与切向力之间的比例关系。因此，在进一步的研究中，可以利用刀具主轴功率来简化过程监测。在接下来的研究中，将开展弹性在切入锥齿轮磨削中的影响，以及能否实现平稳工艺的研究。

　　弹性对切削力过程的影响。在螺旋锥齿轮磨削中，在以前的试验中没有确定固定条件。由于这个原因，下面的部分将检查是否可以随着切削力的增加达到静止状态。随着力的增加，就有可能克服弹性效应，从而实现对复合材料的完整加工。切削力的增加应通过依次增大最大切入深度来实现。目的是确定在螺旋锥齿轮磨削过程中切削量与切削力的关系以及切削力在进给过程中的特征过程。

　　对于每个切入深度，先对一个齿轮进行磨削，然后在测量刀具主轴功率的同时完成所需的切入深度测量。每侧进给量∆s可由切入深度根据式2计算:

　　在研究过程中，最大刀具位置以d=50 um的步长增加。根据公式2，得到As = 17 um的进给工步。每齿侧的总进给量依次增加∆stot = 17-137 um。相比之下，参考过程中最大总进给为∆stot = 50 um。通过增加总进给量，应该确定一个平稳的工艺，从而可以实现平稳水平的切削力。减小了砂轮刀尖半径，避免了在加大切削深度的情况下加工齿根。精加工是以vc= 15 m/s的切削速度和vt=30 mm/min的进给量进行的。在加工每一个齿隙的过程中，主轴功率各种总进给∆stot如图8所示。

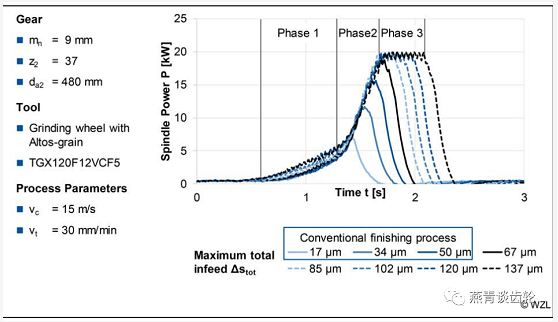
　　从图中可以看出，最大进给量的增加伴随着最大主轴功率的增加。此外，在功率曲线上可以看到三个阶段。在第一阶段，无论最大的总进给∆stot有一个大致线性增长的主轴功率的变化。由于这一阶段发生在砂轮和齿面的初始接触之前，它是由于间隙中的油摩擦导致的。

　　在第一阶段的增长之后，在第二阶段，所有参数都有一个更快的线性增长，这是由于材料去除引起的。对于主轴功率曲线，时间点和梯度具有可比性。

　　对于总进给量最大的∆stot为67 um的变型，在达到最大值后主轴功率迅速增加，随后主轴功率迅速下降到初始水平。对于总进给∆stot≥85 um最大的参数，在主轴功率下降之前，第二阶段主轴功率迅速增加，随后是第三阶段，主轴功率近似恒定。由此可以看出，随着进给量的增加和被加工材料的增加，在切入法锥齿轮磨削中可以达到固定的刀具主轴功率水平。根据之前确定的切向力与主轴功率的比例关系，这意味着切向力在这种状态下也达到了静止水平。这是由于加工条件已经达到，在此条件下，可以加工整个余量。

　　在下面，在切入法锥齿轮磨削弹性变形的帮助下，由齿轮先前执行的变量进给∆stot试验确定。为了能够确定实际加工体积作为最大总进给量的函数，在达到最大切削深度后没有停留时间进行精加工。加工后，确定了所有齿轮的齿厚，并与理论齿厚作为最大总进给量的函数进行了比较。通过这种方法，可以确定每个齿侧的剩余余量∆sR，见图9。

　　浅色的点和回归线代表剩余的余量Asn在每个侧翼的路线，取决于最大的总进给∆stot。可以看出，剩下的余量随着进给量的增加而开始增加，然后趋于平稳。如果将最大进料量设置为∆stot= 137 um，则每齿侧余量∆sR= 16 um。可以假设剩余的余量是由刀具、工件和机床的变形组成的。在未来，这应该通过单独的位移测量进一步研究。图中的暗点表示所有测试点的最大主轴功率P超过最大总进给∆stot。对比发现，剩余余量∆sR与最大主轴功率P成比例增大。最后三个总给最高的测试点有一个近似恒定的剩余余量和近似恒定的最大主轴功率。

　　如果将最大主轴功率P绘制在余量∆sR，就会有一个明显的近似的线性关系，见图9的底部。

　　主轴功率P与切向力Ft成正比，近似与法向力Fn成正比。这种相关性对应于虎克定律的理论，即整个系统表现得像一个刚度k的弹簧。因此，法向力Fn和挠度以及由此产生的剩余余量∆sR之间的关系可以用通常的弹簧近似来描述，见方程3。

　　基于刚度，系统变形和剩余余量∆sR可以预测考虑的测试设置与监测主轴功率。例如，可以通过这种方式设置所需的停留时间。为了能够将确定的关系转移到其他工艺配置中，将来必须更精确地确定弹簧刚度的组成。此外，对于不同的齿轮几何形状，必须验证主轴功率与法向力之间关系的有效性。