编者按：

　　各位粉丝朋友们，欢迎阅读本期小编推送的《汽车驱动桥螺旋锥齿轮齿面测量误差补偿方法》文章。文章主要介绍了提升汽车驱动桥螺旋锥齿轮齿面加工质量对整车的安全与节能性能有重要意义。

　　该文针对汽车驱动桥螺旋锥齿轮实测和理论齿面存在的测量误差，提出了一种基于对偶四元数优化的迭代最近点(ICP)齿面测量误差补偿方法。

　　本篇文章因篇幅较长，特安排两期推送。

　　本期推出：汽车驱动桥螺旋锥齿轮齿面测量误差补偿方法(一)

　　提升汽车驱动桥螺旋锥齿轮齿面加工质量对整车的安全与节能性能有重要意义，该文针对汽车驱动桥螺旋锥齿轮实测和理论齿面存在的测量误差，提出了一种基于对偶四元数优化的迭代最近点(ICP)齿面测量误差补偿方法。将误差补偿问题转化为两曲面的配准问题，利用对偶四元数对齿面配准模型进行表示并得出误差矩阵，将误差矩阵线性化并使用凸松弛的全局优化算法对其实部进行优化，实现螺旋锥齿轮齿面的精确配准。结果表明：螺旋锥齿轮凹齿面的误差补偿率最高达77%，最大误差由补偿前的22.11μm降至5.64μm，平均误差由补偿前的10.34μm降至2.38μm，该算法与传统奇异值分解法(SVD)、四元数法和Levenberg-Marquardt 法(L-M)相比有更高的求解精度和稳定性，证明所提出的补偿方法具有可行性。

　　螺旋锥齿轮是机械设备中关键基础元件之一，广泛应用于汽车、造船、工程机械、建筑机械和交通运输机械等领域。汽车驱动桥螺旋锥齿轮齿面的加工质量直接影响主减速器齿轮传动的噪声、齿轮寿命以及传递效率等，进而影响到汽车的质量和安全性能。精确的齿面测量和误差补偿可以显著提高齿轮的啮合质量，减少能量损失，提升传动效率，降低燃油消耗，促进汽车节能。因此，对驱动桥螺旋锥齿轮齿面测量误差进行分析和补偿具有重要意义。

　　在齿轮测量机测量汽车驱动桥螺旋锥齿轮齿面的过程中，回转轴倾斜和大端端面加工误差等多种因素导致理论齿面与实测齿面存在偏差。韩连福等分析了齿轮测量机的拓扑结构，由拓扑结果采用多体系统理论建立了齿轮测量机几何误差补偿模型。邢元等提出一种基于欧式线性空间的软件误差补偿方法，通过 二级补偿机制有效提高齿面加工精度。宋碧云等基于改进的levenberg-marquardt法(levenberg-marquardt，L-M) 并选取敏感性较高的加工参数对螺旋锥齿轮齿面误差进行补偿。硬件补偿方法成本高且零件测量时出现的误差是不可避免的，软件补偿方法是现在的主流方法，但目前存在计算强度大、迭代不收敛以及误差补偿不够精确等问题。目前最常用的齿面配准方法是迭代最近点算法 (iterative closest point，ICP)，其实质是基于最小二乘法，将最近点迭代并通过更新两组曲面数据的对应关系，实现两齿面的精确配准。LIU Yongsheng等用阻尼Gauss-Newton法代ICP算法中奇异值分解法(singular value decomposition，SVD)来求解几何变换矩阵，有效实现了测量齿面向理论齿面的配准补偿，但其容易陷入局部最优解。ZHOU Lihua等提出了一种匹配点搜索方法，解决了测量齿面与理论齿面之间的对应关系，但其空间复杂度和时间复杂度较高。XIE He等提出了基于点到球面配准的最近邻精细配准算法，将配准问题转化为非线性优化问题，利用Taylor展开式求解配准运动参数，但其需要选择适当的初始参数。

　　为解决现有齿面测量误差补偿方法存在的问题并实现理论齿面与实际齿面偏差的补偿，本文首先进行两齿面之间的配准;针对现有齿面误差补偿方法和ICP算法的局限性，利用对偶四元数在同时处理旋转和平移变换中的优势，提出一种基于对偶四元数优化的ICP迭代误差补偿算法，以解决传统ICP方法容易陷入局部最优解的问题;利用对偶四元数获取误差矩阵，将误差矩阵线性化并进行凸松弛优化，以此提高齿面配准的精度和稳定性;最后通过实测实验验证本文提出算法的有效性。

　　1螺旋锥齿轮齿面测量误差分析

　　汽车驱动桥由螺旋锥齿轮、差速器、车轮传动装置等关键部件组成，作为汽车传递动力的关键组件，其性能和可靠性直接影响整车的动力表现和行驶安全性。 驱动桥螺旋锥齿轮齿面测量误差为实际测量齿面与理论齿面之间存在的偏差。如图1所示，在齿轮轴上建立理论坐标系 {O: X, Y, Z}，螺旋锥齿轮齿面任意 理论测量点Pi与其对应的实际测量点Qi之间的差即为该点齿面偏差δi。当测头到达预设测量位置时，实际测头球心C'i与实测点Qi都在法向量ni方向上，齿面与测头的接触点Qi处于法线方向nQ上，Qi点到Pi点的距离等于实际测头球心C'i与理论测头球心Ci之间的距离di。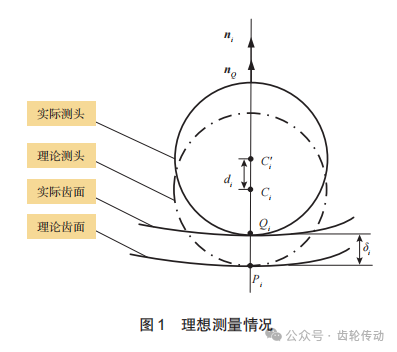

      在实际测量中，螺旋锥齿轮齿面是连续光滑曲面，偏心和倾角误差导致被测齿面与理论齿面不一致，接触点处的法线方向与齿面法线方向并不完全一致。如图2所示，实际测头球心与实际接触点Qi不在ni上，接触点法向nQ与ni也不在同一方向上。理想接触点Pi与实际接触点Qi有一定距离，此时齿面偏差δi为点Pi到点Qi的距离。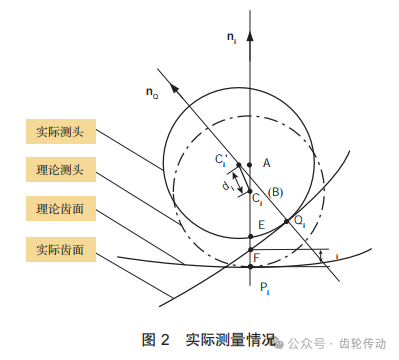

      由几何关系可知：AB与BE的和为测头半径，由于CNC齿轮测量机的测头半径很小，E与Pi的距离非常近，所以PiF的距离近似等于AB的距离，则此时δi的值可以用式 (1) 近似表示：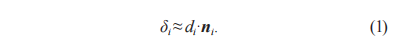

      其中：di为实测球心与理论球心之间的距离;ni为理论齿面的法向量。

　　设理论齿面数据点集为P，由{P1, P2, ⋯Pn} 构成，实际测量数据点集为Q，由{Q1, Q2, ⋯Qn} 构成，齿轮的实测齿面测量点Qi可以由理论齿面数据点Pi 、齿面偏差δi和法向量ni表示，如式 (2) 所示：

      为了减小甚至消除实测齿面与理论齿面之间的偏差，需要实现理论齿面与实测齿面的精确配准，利用配准结果实现螺旋锥齿轮的齿面误差补偿。

　　2传统对偶四元数算法及齿面配准模型

　　对偶四元数的形式与性质：对偶四元数表征旋转矩阵和平移向量的方式与传统方式不同，它们之间存在一定的数学关系。理论点构成的坐标系O和实际测量点构成的坐标系S之间的变换关系可以近似地通过一个平移矢量和一个单位四元数来表示，也可以采用一个更加紧凑和简洁的方式来表示，即单位对偶四元数，如式 (3) 所示：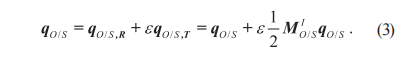

      其中：qO/S, R为对偶四元数的实部;qO/S, T为对偶四元数的对偶部;ε是一个与实数域R垂直的维度单位长度，它满足ε2=0 ;M1O/S=(0, M1O/S) 代表理论坐标系O的原点到实测坐标系S的原点之间的矢量。式(3)也可以简洁表示为式(4)：

      其中：r和s是q的实部和对偶部，且r=r1+r2i+r3j+r4k，s= s1+s2i+s3j+s4k ;单位对偶四元数满足单位性和正交性。任意四元数p和q相乘可以通过矩阵U(p)和W(q)来表示，如式(5) 所示：

      其中，矩阵U(p)和W(q)分别是四元数p和q的四元数矩阵，且U(p)称为W(q)的蜕变矩阵，具体值如式(6)所示：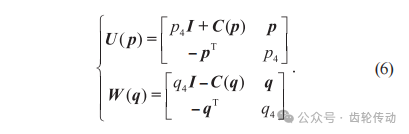

      其中：C(p)为偏对称矩阵，也称为反对称矩阵，

      齿面配准模型：驱动桥螺旋锥齿轮齿面的误差补偿数学模型本质上是三维空间曲面的相似变换，齿面理论测量点集P的空间变换用旋转矩阵R和平移矩阵T表示，经过空间变换得到点集Q'，如式(7)所示：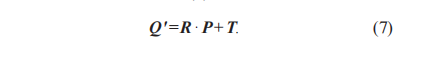

      其中，T是由平移向量t构成的矩阵。

　　点集Q'与实测点集Q的差值即为误差矩阵E，如式(8)所示：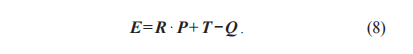

      传统方法选择距离较大的对应点通过奇异分解 (SVD) 方式获得变换矩阵R、T。首先根据参与求解的理论与实际点云的质心构造分解矩阵，将其进行SVD分解，将矩阵正交对角化分解得到2个特征向量矩阵，最后求解得到旋转矩阵R和平移矩阵T。由于螺旋锥齿轮齿面理论点云与测量点云之间的误差较小且一一对应，不存在噪音点，不需要进行控制点的选取过程，且不需要对最近点进行搜索，可采用定向点对点的精配准方式，如图3所示。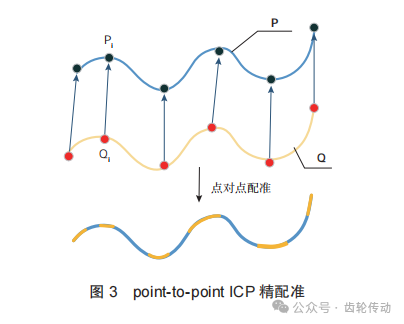

      3对偶四元数优化的ICP迭代算法

　　基于对偶四元数优化的ICP迭代误差补偿算法是以对偶四元数的形式将齿面配准方程分解为旋转矩阵和平移矩阵2部分，获取误差矩阵方程并建立新的问题模型，提取同名特征点并将两点集进行粗配准。为得到更精确的配准结果，将误差矩阵方程线性化并对其中的旋转矩阵进行全局优化，使用MATLAB的Sedemi工具进行凸松弛优化得到全局最优解。根据平均误差、最大误差、误差补偿率和方差验证算法补偿结果的准确性。

　　旋转参数与平移参数的对偶四元数表示：对偶四元数的几何意义可以表示为2个三维集围绕着一个轴做刚体运动，先沿着向量n做平移运动至p'点，平移距离为d，然后在p'点绕向量n旋转θ角度到pS点，如图4所示。

　　式(4)可以由图4的几何关系重写，如式(9)所示：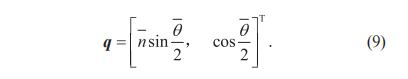

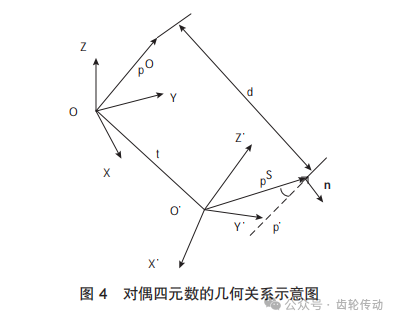
      其中

      式(4)中的实部r和对偶部s与式(9)中n和θ的关系如式(10)所示：

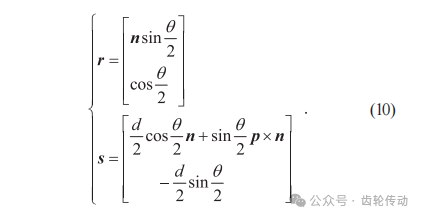
      因四元数法能保持方程是线性的且不产生奇异，任何三维空间的向量都可以用实部为0的四元数表示，所以引入2个以坐标向量为正值的纯虚四元数，如式(11)所示：

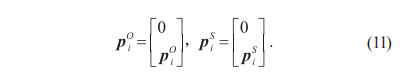
      将纯四元数p经过四元数r旋转变换到p'，如式(12)所示：

      其中，W(r)TU(r)可拓展为矩阵

      平移四元数t'的表示如式(13)所示：

　　而式(8)可以用对偶四元数重新表示，如式(14)所示：

      其中：pOi =(xOi , yOi , zOi)T与pSi=(xSi ,ySi ,zSi)T 表示理论测量点与该点对应的实际测量点的控制向量;W(r)TU(r)为旋转矩阵;2W(r)Ts为平移矩阵;λ为比例因子。在螺旋锥齿轮齿面误差补偿算法中，理论齿面和实测齿面的整体大小的差别很小，因此本文中涉及的比例因子λ近似为1。

　　将式(14)进行线性化，从实测齿面数据点与理论齿面数据点中提取同名特征点，可以得到误差方程， 如式(15)所示：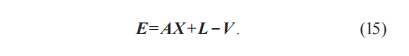

      其中：E=(ex, ey, ez)T ，V=(vx, vy, vz)T ，X=(dr1, dr2, dr3, dr4, ds1, ds2, ds3, ds4);A是根据KD-tree搜索出的点坐标构成的矩阵;L是与A同名特征点对应的矩阵。

　　旋转矩阵的全局优化：在实际测量中，汽车驱动桥螺旋锥齿轮测量齿面与理论齿面的质心相差不大，优化两齿面间的平移向量对最终误差补偿效果的影响甚微，所以本文仅针对旋转矩阵进行全局优化。神经网络、模拟退火、禁忌搜索等启发式全局优化算法具有广泛的适用性，但通常需要调节多个参数以实现最佳性能，分支限界法的技巧性更强，由于具体问题的差异，分支限界法的具体实现方法并不具有普适性。凸优化方法是通过将目标函数转化为阶数更低的凸函数 ，将可行区域转化为凸包络，使多极值非凸优化问题转化为凸优化问题求解。针对低阶(二次)的非凸函数优化问题，既能保证执行效率，又能保证求解的最优性。凸松弛优化方法最初由D. Hendon等将其应用于测算机器视觉中的三维重建问题，常用于机器学习、 电力系统等领域，该算法的优点是初值不需预估便获得最优解。为了最大限度确保每次求解的优化结果都能收敛到全局最优解，本文提出将对偶四元数与凸松弛优化算法结合进行求解。为了避免求解过程中出现2个最优解的情况，同时确保特征点求解的数值稳定性，增加约束条件 r·sT=0和rT·r=1，并在确定松弛系数后，利用线性矩阵建立凸优化模型。以最小化方程式(8)为几何误差目标函数，以对偶四元数的性质为约束条件，建立二阶多项式优化问题并进行优化，具体步骤如下。

　　步骤1：确定最大迭代次数，定义对偶四元数变量：r=(r1, r2, r3, r4)T ，s=(s1, s2, s3, s4)T，初始值 r=(1, 0, 0, 0)T，s=(0, 0, 0, 0)T，建立目标函数minf(r)，如式 (16) 所示：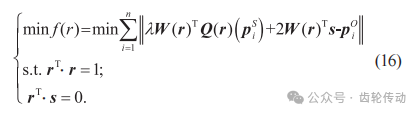

      步骤2：确定松弛系数，将线性化后的式(15)引入，确定凸优化模型，如式(17)所示：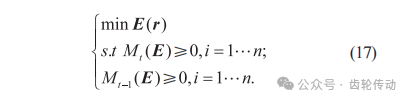

      其中，当Mt(E)与Mt-1(E)满秩时，才能得到全局优化解，进行下一步。

　　步骤3：通过调用线性优化求解器Sedumi工具箱得到最优解，进而得到对偶数实部 r。

　　步骤4：将得到的r代入式(17)中得到对偶部s。

　　步骤5：输出对偶四元数q。

　　旋转矩阵的凸松弛优化流程如图5所示。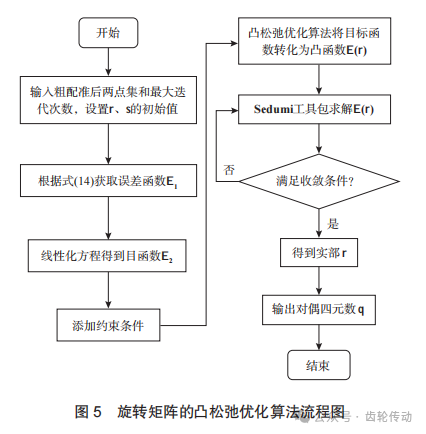

      对偶四元数转换坐标的精度计算：

　　确定参数精度的必要性在于确保对偶四元数模型的可靠性和准确性，便于有效地描述和预测复杂算法的行为。基于对偶四元数优化的ICP迭代算法获得的最终结果，需要通过计算精确度来验证算法的有效性。设理论点集P和测量点集Q对应各点的欧式距离为fi'，由此得出对应点的欧式距离和F0=Σfi'，将基于对偶四元数优化的配准算法与现有文献提出的其他配准算法的结果进行对比。本文将算法配准后最小欧氏距离和Fmin设定为最终误差。在此基础上定义B为整体误差补偿率来验证算法的精确度，如式(18)所示：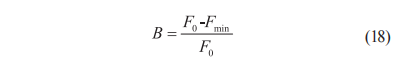

      进一步定量分析配准的精度，引入平均误差和方差s2E，

是指补偿后齿面对应点之间距离的均值，可以评判补偿算法的优劣性，s2E 是对应点之间距离与均值之差的平方和的平均值，可以反映各点补偿结果的离散程度。